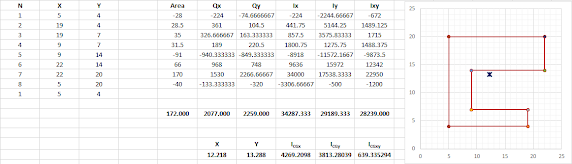
Calculo de Áreas, Primer Momento, Centroides y Segundo Momento de un Polígono.
Área
El problema de determinar el área de un polígono parece, en
el mejor de los casos, complicado, pero la fórmula final es particularmente
simple. Considere un polígono formado por segmentos de línea entre N vértices
(xi , yi), i = 1 a N. Se supone que el último vértice (xN
, yN ) es el mismo que el primero, es decir, el polígono está
cerrado.
Nota para polígonos con agujeros. Los huecos suelen
definirse ordenando los vértices del polígono circundante en dirección opuesta
a los de los huecos. Este algoritmo todavía funciona, excepto que el valor
absoluto debe tomarse después de agregar el área del polígono al área de todos
los agujeros. Es decir, las áreas de los agujeros serán de signo opuesto al
área del polígono delimitante.
El signo de la expresión de área anterior (sin el valor
absoluto) se puede usar para determinar el orden de los vértices del polígono.
Si el signo es positivo, los vértices del polígono se ordenan en sentido
contrario a las agujas del reloj con respecto a la normal, de lo contrario, en
el sentido de las agujas del reloj.
Centroide
El centroide también se conoce como el "centro de
gravedad" o el "centro de masa". La posición del centroide
asumiendo que el polígono está hecho de un material de densidad uniforme se da
a continuación. Como en el cálculo del área anterior, se supone que xN
es x1,en otras palabras, el polígono está cerrado.
Segundo momento de un polígono
Lo siguiente asume vértices de polígono orientados en
sentido antihorario, use el valor negativo para polígonos en sentido horario.